钣金切割工艺技术研究

1 饭金切割工艺技术研究
1.1 饭金相关切割工艺概述
    在采用数控火焰切割机进行钢板下料的生产中，选择合理的工艺方案，适当的切割顺序、切割方向和切割起点，是保证零件切割精度与切割效率的关键。例如在进行多零件套料切割时，应遵循“先割小、后割大，先割里、后割外”的原则；为了提高切割效率，提高材料的利用率和切割速度，降低生产成本，采用共边切割，即使两个或数个能够搭边的零件并接在一起进行切割，这样就可以减小切割的路径长度；在对长条或面积比较大的薄板零件进行切割时，为了防止切割时零件由于受重力和热的作用而发生变形导致切割误差变大，甚至产生废品，采用了搭桥的工艺方法，即是在一个零件的切割周边上设置几个暂不切割点，这几个点在切割过程中将零件与钢板连为一个整体，最后再切割开这几个点，可防止割跑零件，减小零件长度方向上的收缩变形。
 
    另外，还要注意切割过程中热量传导的连续性问题。钢材的氧气切割是利用气体火焰(称预热火焰)将钢材表层加热到燃点并形成活化状态，然后送进高纯度、高流速的切割氧，使钢中的铁在氧氛围中燃烧生成氧化铁熔渣同时放出大量的热，借助这些燃烧热和熔渣不断加热钢材的下层和切口前缘使之也达到燃点，直至工件的底部。与此同时，切割氧流的动量把熔渣吹除，从而形成切口将钢材割开。由此可以推断，在火焰切割过程中，割嘴走过的路径必须连续，以使得割嘴将要切割的小范围钢板的温度始终保持恒定，否则就会造成热量的不连续，使得切割失败。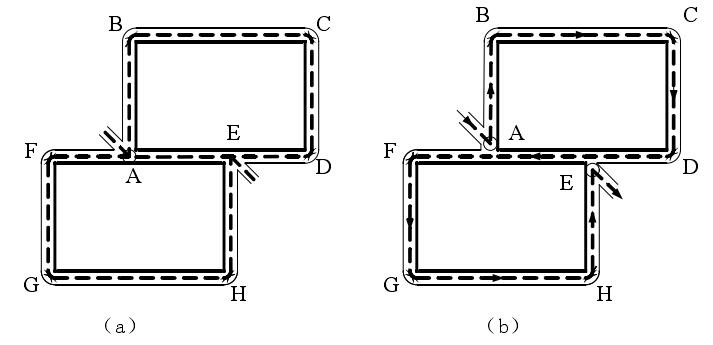
 
图4.1热量连续条件对切割路线的影响
 
    如图4. 1所示的两个共边零件的切割，如果选择4.1(a)图所示的切割方式，假如选择切割路径为A-E-D-C-B-A-F-G-H-E，当切割完上面第一个零件，割嘴又走到A点的时候，切割路径就发生了断开不连续的情况。同样道理，选择切割路径为A-B-C-D-E-A-F-G-H-E，还是会发生同样的热量不连续的情况。解决办法就是如图4.1(b)所示的将切入点A和切出点E分别往上往下移动一个割嘴直径的距离，并且选择A-B-C-D-F-G-H-E的S状的切割路径，就可以避免热量不连续的问题。
 
1.2 共边切割
    本文研究的共边切割是人机交互式的共边切割。其过程是先由用户对要共边切割的两个零件进行共边平移，使两个轮廓的形成一条公共边，当然这之前还要对两个零件的轮廓进行等距放大或缩小。
 
1.2.1 共边切割中的割缝补偿技术
    在共边切割时，如果不对两个共边的轮廓进行等距放大或缩小，就会产生过切问题。割嘴在切两个轮廓的公共边时，即使使用机床的刀具半径补偿指令，也会使其中一个轮廓过切，这是因为数控机床的半径补偿指令在对一个零件的轮廓进行切割时不会考虑是否切割到了另外一个轮廓的内部，在对两个共边的轮廓切割时必然会使其中一个轮廓过切。
 
    由此，共边切割引入了割缝补偿技术，考虑两个外轮廓的情形，割缝补偿技术就是把两个轮廓都进行等距放大或缩小一定的距离(对外轮廓放大，对内轮廓缩小，这个距离一般是火焰切割机割缝宽度的一半△/2)，再把等距放大了的轮廓进行平移使之搭边，不使用机床的刀具半径补偿指令，切割出来的轮廓大小就是图纸上设计的零件轮廓的大小。如图4. 2所示。割缝补偿包括两个方面的内容：等距放大(缩小)和轮廓相邻图素的转接。

 
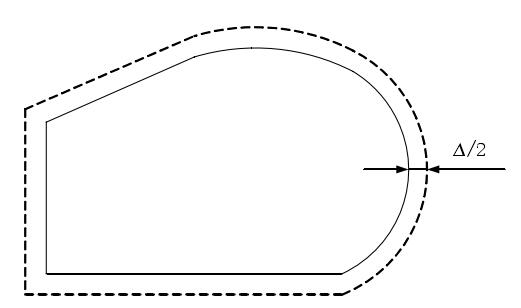
图4.2 割缝补偿

 
    一般而言，当图形比较简单(外凸)或放大量较小时，等距线的生成算法比较成熟。当某些图形为内凹情况时，如果等距放大量超过了极限距离，该图形的内凹部分将发生干涉。这就要对放大了的图形进行判断和处理。 目前的CAD系统中，应用最广泛的曲线一般还是直线、圆和圆弧，其等距放大的公式可以进一步表示为图4.3(a)和(b)的形式。

 
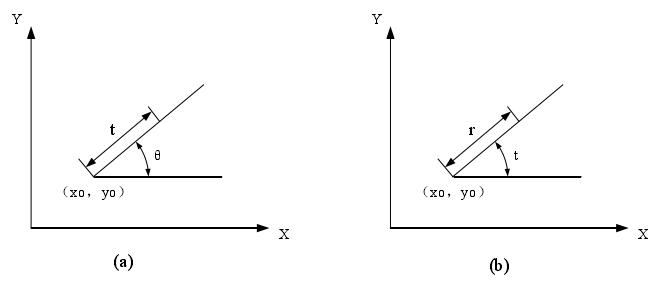
图4.3直线和圆的等距放大

 
2 干涉问题的解决
    当图形出现内凹的情况下进行等距缩放时，如果放大的距离大于极限距离时，等距图就会发生自交，将会发生干涉错误，如图4.4所示。

 
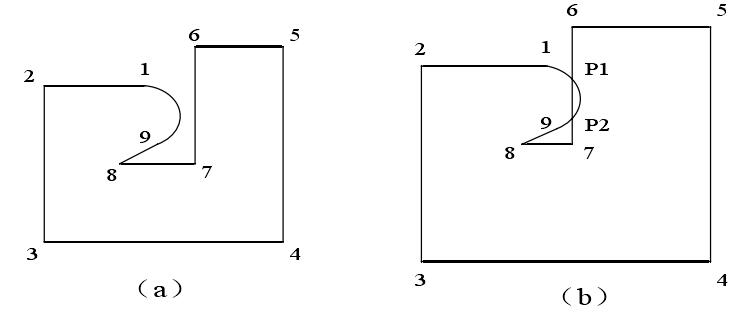
图4.4等距放大干涉问题的解决

 
    解决上述错误有两种途径。其一是在进行等距放大之前，进行计算，判断在给定的放大距离时是否会产生干涉现象，如果发生了千涉，则进行一定的处理以简化原图，然后再进行等距放大。另一种方法则是先按照上面介绍的方法计算出等距放大后的图形，然后再判断是否有干涉发生。如果发生了干涉，则删除某些交点、线。其基本思想就是寻找独立的封闭图形，然后求取面积最大的一个作为等距放大后的结果图形。第一种方法面临的困难是很难找到发生干涉的判据。这里采用第二种方法。
 
    (1)编号。按逆时针方向给图形上的各个顶点(圆弧仅计首尾两点)顺序编号，并将其存放到双向循环链表 source之中，然后计算得出等距放大后各顶点对应的新顶点，也将它们存放在另一双向循环链表：esult中，如图，此二链表的结点均为1、2、3、4、5、6、7、8、9。
    
    (2)寻找等距放大图中多余的交点。按照链表result中节点的顺序遍历各曲线段(或直线段，以下同)，以判断其是否与不相邻的其它曲线段相交，如果产生了交点，则记录该交点，并存放到一个新的单向链表points之中，之后将points中的各个节点插入到result链表中，插入时每一交点都会插入两次。
 
    具体规则为：该交点是由哪两条曲线段相交产生的，就将其分别插入到每一条曲线段所对应的两个顶点之间。如图4.4(b)中的P1点是由曲线段1、9和直线段6、7相交产生，则P1应分别插在顶点1、9之间和6、7之间。点插入之后，再按照新的result链表继续遍历下去(不必重头遍历)，以使后继的所有多余交点都能够准确地插入到result中。
 
    (3)删除某些多余点。沿points链表中点的记录顺序，遍历result链表，进行拆链的工作。由于points链表中的每一个记录都对应着result链表中的两个记录，因而可以将result链表按照points链表中的每个记录分解成两个双向循环链表，记为Result1，和result2，具体拆分规则为：在result中找到与points链表中相应的点后，双向搜索，直至在每个方向上都再次遇到该点为止。

 
3 割缝补偿的转接形式和过渡方式
    根据切割过程中前后两段图素线型的不同，相应割嘴中心轨迹也会有不同的转接形式，对于大部分轮廓的图素，应用最多的还是直线和圆弧，它们有以下四种转接形式：直线与直线转接；直线与圆弧转接；圆弧与直线转接；圆弧与圆弧转接。
 
    为了便于说明问题，这里规定了矢量夹角a，它的含义是指两段图素在交点处非加工侧的夹角。根据a的大小不同，割嘴中心轨迹从一编程段到另一个编程段的段间连接方式即过渡方式有以下3种：伸长型、缩短型、插入型。

 
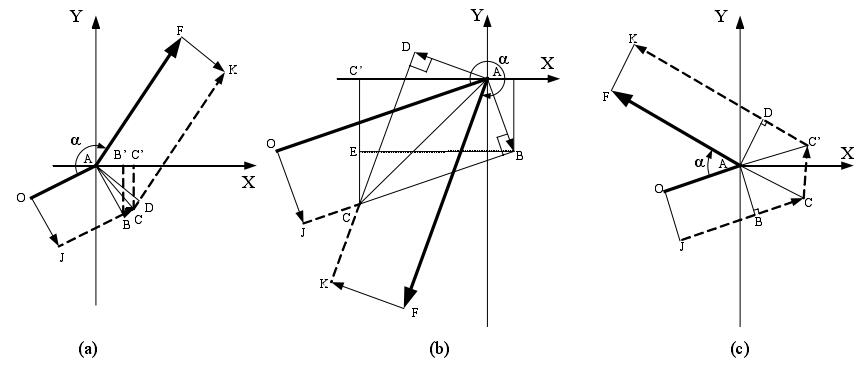
图4.5割嘴中心轨迹的过渡方式

 
4 割嘴中心轨迹的计算
4.1 共边切割的实现
    在对两个轮廓进行共边切割的准备工作完成之后，就可以生成切割轨迹了。当然，这里还必须要有相应的条件判断，找到共边的图素。为简化问题，这里只研究了直线共边的情形。共边切割的实现过程如下：
 
    (1)判断轮廓方向。如果是两个外轮廓共边，且它们不相互包含，则只有它们的轮廓方向相反才能共边切割，否则，提示用户不能进行共边切割；如果是一个内轮廓和一个外轮廓共边切割，且前者包含后者，则只有它们的轮廓方向相同才能进行共边切割，而且只能先切割位于内轮廓内部的外轮廓，否则，也提示用户不能进行共边切割。这是因为在对两个轮廓进行共边切割时考虑到热量连续的因素，必须让割嘴走S形的路线。
 
    (2)寻求公共边。两条直线有搭边的条件是：两条直线11和12斜率相同；11和12的四个端点中有在对方直线段上的情况。例如，11的两个端点start和end至少有一个在12上或者12的两个端点至少有一个在11上。符合这两个条件的直线必然会有搭边。首先对两个轮廓的各个图素进行遍历，搜索到直线元素后就进行上面两个条件的判断，判断为真就分别记录两个轮廓的直线元素11和12，否则就提示用户两个轮廓没有公共边，不能共边切割。
 
    (3)按搭边的线段修改轮廓链表。在找到两个轮廓out1和out2的共边直线段11和12以后，寻找11和12的搭边直线段，也就是寻找它们的公共部分。因为两条直线都是有起点有终点的有向线段，长度又不能确定，因此它们的搭边可以分为如图4.6所示的12种情况，其中A， B为分别为第一条线段(粗线表示)的起点和终点，C，D为第二条线段(细线表示)的起点和终点。
 
    在每种情况下，先要求出两条线段的公共搭边的线段，再以此修改两个轮廓的图素链表。这里以图4.6(10)为例，第二条线段的两个端点C和D都在11的中间，只需要修改out1的图素链表就可以了。其修改方法是，首先分别以点A，C和点D，B为起始点和终止点，生成两个新的直线元素AC和DB，然后将这两个图素分别插入在out1原来的直线图素AB的前面和后面，最后将图素AB的起点和终点修改为C和D两点的坐标，这样，out1原来的图素AB就变成了三个图素。

 
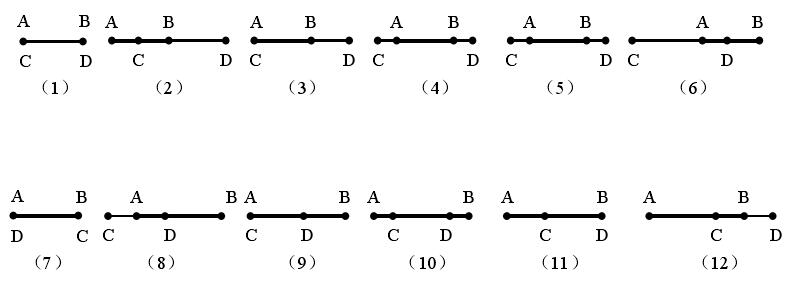
图4.6 两条直线段的搭边

 
    (4)添加引入引出线，生成切割轨迹。考虑到切割热连续的因素，两个零件共边切割时，要合理的安排引入引出线。如图4.7所示，如果左面的轮廓为顺时针，右面的轮廓为逆时针，而且切割顺序是先左后右，则切割轨迹的生成过程如下：

    1.确定两个轮廓的切入点和切出点，因为两个轮廓的时针方向及切割顺序已经确定，则两个轮廓的切入点和切出点也都确定了下来，如图中的b点和k点，这里不能将切入点放在ef上，那样就意味着先切割公共边fg，而先切公共边是不符合切割热连续的工艺要求的。另外要注意的是，切入点和切出点要偏移公共边端点半个搭边。

    2.增加引入线。引入线的长度可以预先设定，其方向按照两个轮廓链表分别紧邻公共边的两个图素的夹角来确定，引入线与该夹角的角平分线相平行，如果紧邻公共边的两个图素有圆弧的情况出现，就取圆弧的切线方向与另一个图素的切线方向来确定它们之间的夹角。

    3.按照顺序分别遍历两个轮廓链表，生成相应的轨迹链表。第二个轮廓的轨迹只能到公共边的前一个图素的末尾结束。

    4.增加引出线。引出线的方向和引入线的方向用同样的方法确定，其长度也可以预先设定。如图4.7，两个轮廓进行共边切割的最终轨迹为：a-b-c-d-e-f-g-h-i-j-k-1。

 
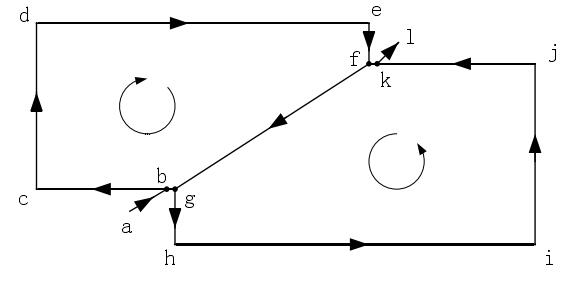
图4.7共边切割轨迹的生成

 
4.2 规则均布零件的共边切割
    在实际生产中，有时会用到大量形状规则的零件，如三角形和矩形等，在套料时可以将这些零件排在一起，对这些零件的公共部分只需要进行一次切割，如图4.8中(a)和(b)，这样也可以大大的提高生产效率，节约生产成本。

 
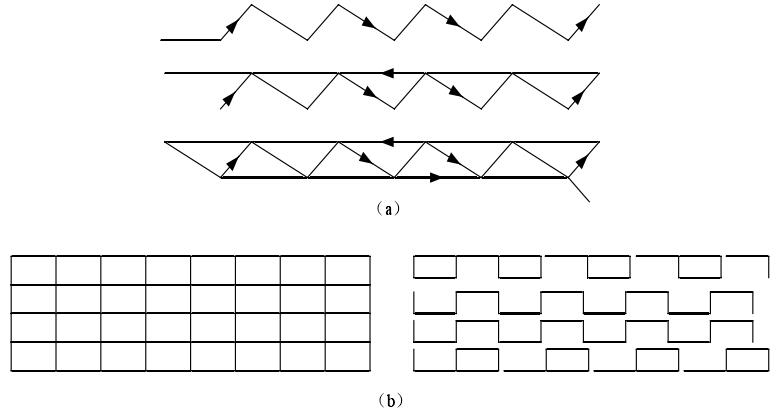
图4.8规则均布零件的共边切割

 
4.3 切割搭桥
    在切割长宽比较大的零件时，零件很容易受到重力和热力作用发生切割变形，采用切割桥工艺可以很好的缓解这种切割变形。为了用户使用方便，系统提供了自动和手动两种形式的搭桥方法。在自动模式下，用户预先指定要切割的零件轮廓和切割桥的长度、宽度以及要使用的切割的数目，系统就会根据轮廓的属性(内外、方向等)，自动将切割桥均匀分布在轮廓上。当然，由于零件的形状变化多端，均布的切割桥不一定满足力学的要求，系统给用户提供了手动搭桥的功能，用鼠标点击轨迹就在相应的部位就生成一个切割桥。图4.9给出了一个应用切割桥的示例。

 
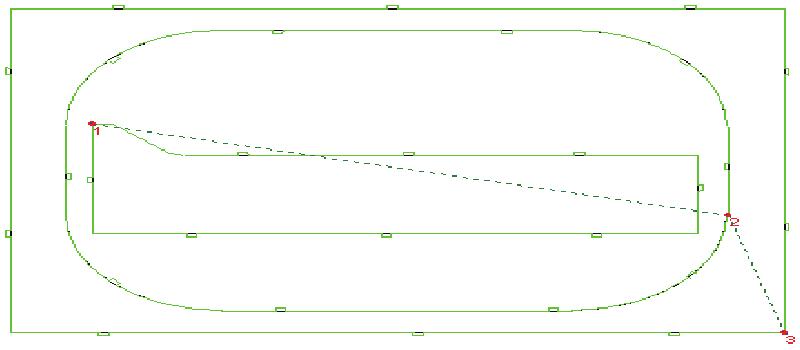
图4.9切割桥应用示例

 
4.4 轨迹连割
4.4.1 轨迹连割的意义
    为了提高切割效率，改善因频繁起弧而引起割嘴寿命和加工质量的降低，在优化排样时，按照一定规则将零件的切割起点尽可能的排列在一起，在经过轨迹连割以后，这些零件的外轮廓只需要一次起弧就能连续切割下来。如图4.10所示，A，B，C三个零件局部相邻，起弧点设在。处理零件的切割顺序为o-a-b-c-d-a-e-f-g-h-e-i-j-k-l-i。本文仅考虑外轮廓的情况。显然，这样会造成部分无用的切割轨迹，但这部分无用轨迹的长度可以设定。

 
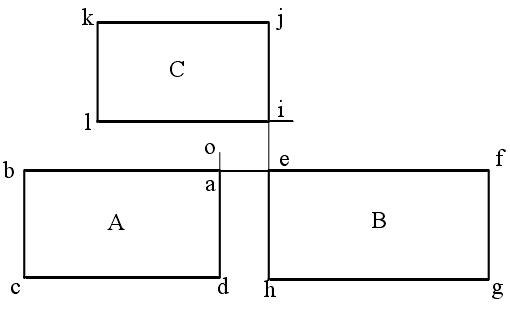
图4.10轨迹连割图示

 
4.4.2 轨迹自动连割的具体实现过程
    在自动识别某组零件是否可以多轨迹连割时，要同时考虑几个条件：
    (1)两个零件不被其他所有零件嵌套并且他们之间也没有嵌套关系；
    (2)第一个零件的终点与第二个零件的起点之间的距离小于预先设定的值；
    (3)用于连接两个轨迹的直线不得与所有零件相交；
 
    如果两个轨迹能够同时满足以上三个条件，就把trace j所指轨迹的起点连接到trace i所指轨迹的终点上，即将trace j和trace i合并为一段新轨迹，并将这个新轨迹的指针赋予trace i，同时将trace j从数组中去除，trace j+1占据trace j的位置，数组大小减1。然后，判断trace j及其以后所指的轮廓是否满足条件，直到数组结束。将i增加1，重复以上过程，直到数组结束。具体流程见图4.11。
 
    为了简化问题，这里先讨论讨论两个轨迹均不被其他轨迹包容的情况。要判断一个封闭的轨迹是否在其他封闭的轨迹之内，只要判断该封闭轨迹的起点是否在其他封闭轨迹之内，这就是点的包含性检验问题，对于起点在其他轨迹之外，而其部分图素又在其他轨迹之内的情形，可以由轨迹干涉的功能来判断。下面就来研究一下点的包含性检验问题。

 
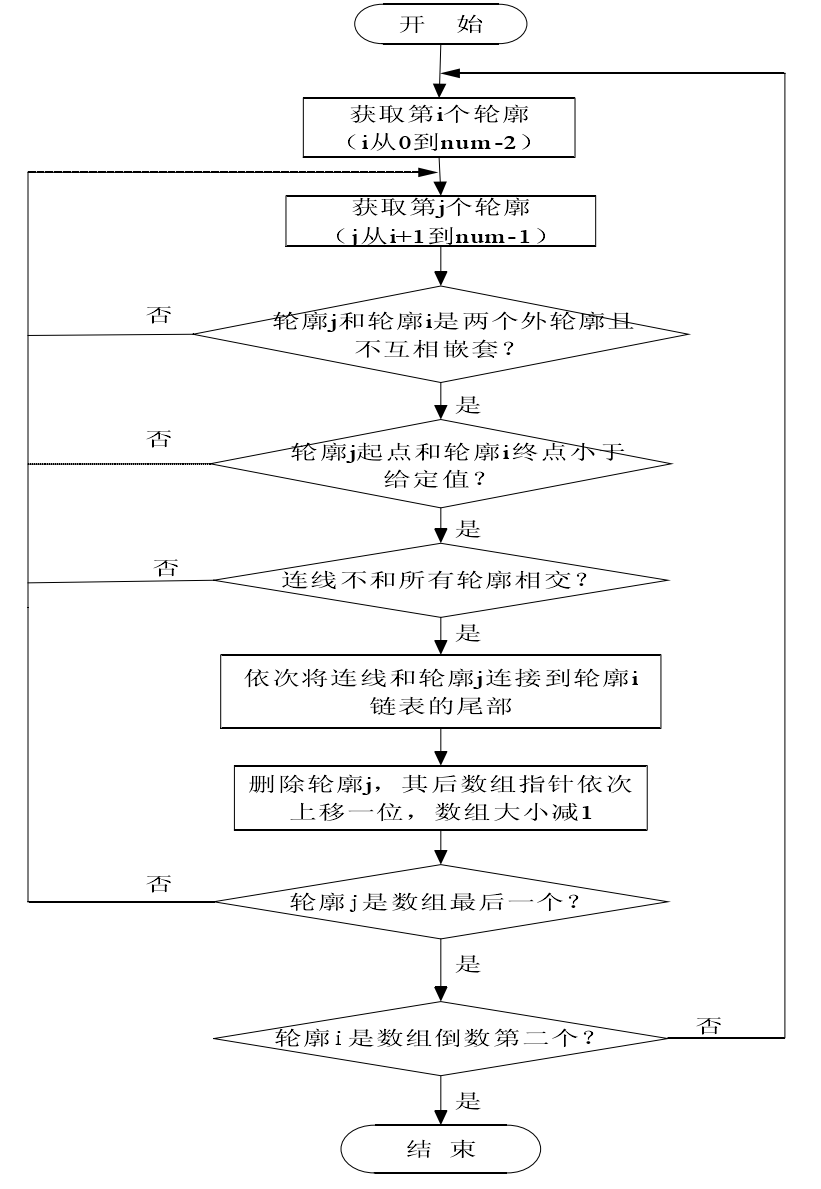
图4.11轨迹连割流程图

 
  点的包含性检验是指一个点是否包含在某一个区域内。在这里，把这个区域定义为一个多边形。常用的检验方法有两种：夹角和检验法和交点数检验法，考虑到后者的奇异性问题，本文采用前一种检验方法。
    
如图4.12所示，设有一个点P和一个多边形ABCDE。依次将点P分别与多边形各顶点A、B、C、D、E相连，令ai为多边形各相邻两顶点与点P相连所形成的夹角。例如在图4.12中：a1=∠APB，a2=∠BP，a3=∠CP，a4=∠DPE，a5=∠EPA。

 
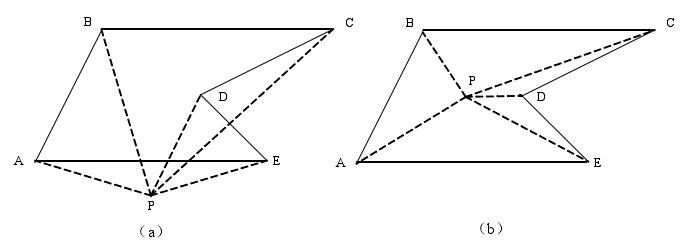
图4.12夹角和检验法

 
    在轮廓不存在圆弧及圆的图素的情况下，上述结论是正确的。但轮廓在有圆弧或圆的情况下，就要对圆弧及圆进行离散，然后再进行判断，否则就会出现问题，如图4.13所示。

 
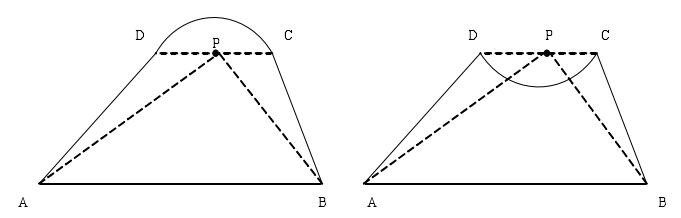
图4.13夹角和判断法有圆弧的情况

 
    如果在内存中只有A，B，C，D四个点的坐标值，判断就会出现∠CPD是兀还是一兀的歧义。为解决这个问题，就要对圆弧进行离散。如图4.14所示，圆弧离散的过程如下：首先判断判断A，B两点在数组data中的存储次序，取靠前的一点，例如A点。然后以C点为圆心，点A向点B的方向移动到Pi，移动角度定△ai=8兀/180；求出Pi点的坐标，存入数组data；再以Pi，为基点向点B的方向移动到pi+1，求出PI+1，的坐标并将其存入数组data，依次类推，直到B点结束。点Pi的坐标可以由公式4.1来计算(公式中n为点的移动次数)。对于圆，可以采用相似的方法解决。

 
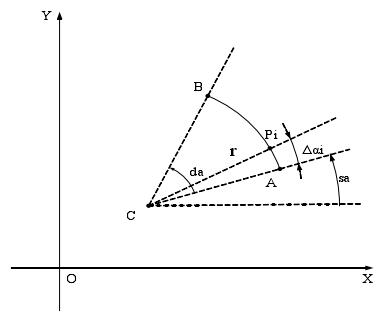
图4.14圆弧的离散

 
点的包含性检验具体过程如图4.15所示：
    对于连线和其他轨迹相交性的判断，可以由其与其他轨迹各个元素的相交性情况来判断。这可分为三种情况进行讨论：直线与直线；直线与圆弧；直线与圆。当然，为提高运行效率，可以先判断连线与其他轨迹最大包容举行的相交性，如果相交，在进行下一步各个元素的判断，否则就转向下一个封闭轨迹。

 
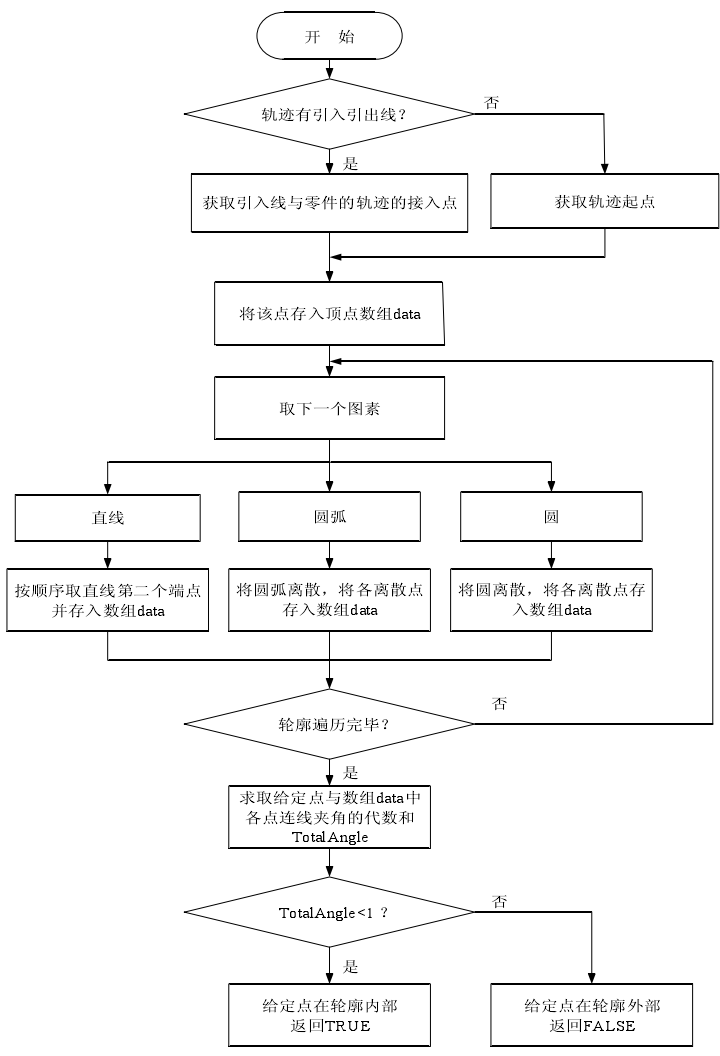
图4.15点的包含性检验流程

 
    图4.16给出了一个轨迹连割的具体实例，图中的7个轮廓采用轨迹连割以后只需要4个引弧孔就可以切割下来了。

 
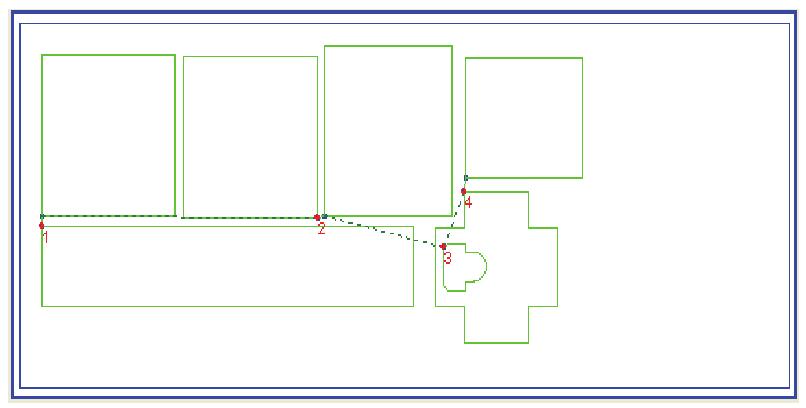
图4.16轨迹连割示例

 
4.5 单个零件切割路径的优化
    单个零件一般具有多个内轮廓特征，这类零件主要由首尾连接的直线、圆弧、圆等图元构成的多个封闭轮廓图形组成。切割机要切割完所有的内环和外环才能完成一个零件的切割任务。切割内环或外环时，首先以一个环上的某一顶点为预热打孔点，打穿再切割完该环，按实际切割工艺，切割顺序应该遵循先内环后外环的原则。要遍历完所有的打孔点完成切割有很多条路径可以选择，割嘴路径优化的目的就是要尽可能的寻找一条最短的路径，以减少切割机空行程的长度，提高生产效率。
 
    当打孔点确定以后，单个零件切割的路径优化问题就是典型的旅行商问题(TSP)。TSP问题是典型的NP完全问题，这类问题随着问题规模的扩大，求解问题的空间、时间复杂度呈指数级的增长，在现有条件下使用常规的方法求解是无法实现的。
 
    自然界一直是人类创造力与智慧的源泉，近年来，许多学者模仿自然界生物的趋优机制，提出了许多仿生算法。目前较为常用的仿生算法主要包括禁忌搜索算法(Tabu Searching，TS )、模拟退火算法(Simulate Anneal，SA)、遗传算法(Genetic Algorithms，GA)、人工神经网络算法(Aritifical Neural Network，ANN)、动态规划，以及最近的蚁群算法((Ant Colony Optimization，ACO)等等。
 
    遗传算法是一种借鉴生物界自然选择和自然进化机制的高度并行、随机的、自适应性的搜索算法，但它存在收敛速度慢、容易陷入局部优化导致搜索停滞的缺点。模拟退火算法是局部搜索算法的扩展，它不同于局部搜索之处是以一定的概率选择邻域中费用值较大的状态，理论上来说，它是一个全局最优算法，但是在搜索过程中，模拟退火算法需要精确的调整接受退火结果的条件，因此往往需要多次计算才可以得到满意的结果，不便于实际应用。
 
    人工神经网络是由人脑的结构得到启发而建立的一种仿生算法的模型，在组合优化问题中，神经网络可以近似的解决问题，它只需要对变量空间、约束、目标函数的描述，而不需要任何清楚明确的代码程序。它的缺点是存在网络收敛速度慢、易陷入早熟、并且参数选择对求解结果影响很大的缺点。
 
    与前面几种算法相比，蚁群算法虽然也容易陷入停滞，但是蚁群算法并行性较强，个体间不断进行信息交流和传递，有利于发现较好的解。单个个体容易收敛于局部最优，多个个体通过合作可以很快收敛于某个子集，有利于对解空间的进一步搜索，从而发现较好的解。并且蚁群算法模型简单，算法参数设置简单，便于实际应用。
 
4.5.1 基于蚁群算法的路径优化
4.5.1.1 蚁群算法原理
    蚁群算法是由意大利科学家Marco Dorigo等人在20世纪90年代初提出来的。它是继模拟退火算法、遗传算法、禁忌搜索算法、人上神经网络算法等启发式搜索算法后的又一种应用于组合优化问题的启发式搜索算法。单个蚂蚁的行为极其简单，但它们所组成的蚁群群体却表现出极其复杂的行为。
 
    它们在找食物时，总有能力找到一条从食物源到巢穴之间的最优路径，并能随环境的变化而变化，适应地搜索新的路径，产生新的选择，这是因为蚂蚁在寻找路径时会在路径上释放一种特殊的信息素。当他们遇到一个还没有走过的路口时，就随机地挑选一条路径前行，同时释放与路径长度有关的信息素，路径越长，释放的信息素浓度越低。当后来的蚂蚁再次遇到这个路口时选择信息素浓度较高的路径概率就会相对较大，这样大量蚂蚁组成的蚁群行为便形成了一种信息正反馈现象。
 
    最优路径上的激素浓度越来越大，而其他路径上的信息素浓度却会随时间的流逝而消减，最终整个蚁群会找到最优路径。不仅如此，蚂蚁还能够适应环境变化，当蚁群运动路线上突然出现障碍物时，蚂蚁能够很快地重新找到最优路径。
 
4.5.1.2 割嘴切割路径的调整
    数控切割机是由计算机采取实时控制来完成自动切割的，它只是严格地按照数控程序进行工作而不管下面钢板的变形与位移等，火焰切割的性子决定了在对钢板进行切割是要产生大量的切割热，这些热量会引起钢板的变形，于是，在切割过程中如果不采用相应的工艺方法就会产生切割的误差，甚至会造成废品。

 
4.6 本章小结
    本章研究并实现了饭金切割中几个比较实用的切割工艺，如共边切割，搭桥切割，轨迹连割等。针对切割轨迹规划问题，提出了基于蚁群算法的分步规划的方法，其优点在于保证切割工艺“先割小后割大”的前提下减少切割机空行程的长度。